Introducing multiple imputation and the associated between-sample variance

Biostats
Author

Imanol Zubizarreta

Published

March 10, 2024

Code 
library(dplyr)
library(tidyr)
library(ggplot2)
library(mice)
library(ggExtra)

Objectives

The main objectives of this post are:

  • To showcase how a single imputation method may not be the best approach to handle missing data under MAR. We will be using the data sets obtained in this post where missing data was simulated in the OUT variable conditional on the AGE variable, under MAR. I would recommend going over this post first to review the MCAR, MAR and MNAR concepts.
  • To understand how multiple imputation (MI) method can help us solving the issues we will be seeing with a single mean imputation method (to get unbiased estimates and to account for uncertainty due to missing data under MAR).
  • To understand how the multiple imputation method accounts for the uncertainty due to missing data with the between-sample variance.
  • To present the three main steps in the Multiple Imputation (Rubin’s Rules), and to show how we can go over these steps by using mice::mice function.

Creating some functions

Let me define a couple of functions that I will be systematically using throughout the post.

Code 
tidy_estimates_df <- function(df) {
  df %>%
    cbind(data.frame(param = c(
      "point_est", "se", "ci_lower", "ci_upper"
    ))) %>%
    as.data.frame() %>%
    tidyr::pivot_longer(
      cols = c("prop20", "prop40", "prop60", "prop80"),
      values_to = "Value",
      names_to = "missing_prop"
    ) %>%
    pivot_wider(id_cols = "missing_prop",
                values_from = "Value",
                names_from = "param")
}

plot_estimates <- function(df,
                           title = "Point estimates by starting missing proportion",
                           xlab = "Starting missing proportion (pre-imputation)",
                           ylab = "Point estimate and 95%CI",
                           imputations = FALSE,
                           group = NULL,
                           type_marginal = "density") {
  p1 <- ggplot2::ggplot(df,
                        aes_string(
                          x = ifelse(imputations, "imp", "missing_prop"),
                          y = "point_est",
                          group = group,
                          col = group
                        )) +
    geom_point() +
    theme_bw() +
    geom_errorbar(
      aes_string(ymin = "ci_lower", ymax = "ci_upper"),
      width = .1,
      linetype = 1
    ) +
    labs(title = title, x = xlab, y = ylab)
  
  if (imputations) {
    p1 <- ggMarginal(
      p1 + theme(axis.text.x = element_text(
        angle = 90,
        vjust = 0.5,
        hjust = 1,
        size = 5
      )),
      margins = "y",
      groupColour = TRUE,
      groupFill = TRUE,
      type = type_marginal
    )
  }
  
  p1
}

Analysis data sets

The three variables of our analysis data sets are the following ones:

  • Subject variable.
  • Normally distributed continuous age variable.
  • Outcome variable that is positively correlated with the age.

The following list of length 4 contains the data sets with different proportion of missingness (20, 40, 60, 80%) in the OUT variable that we generated here.

Code 
amp_df_list <- readRDS("../stats_ampute/amp_missing_df_list.rds")
names(amp_df_list) <- c(paste0("prop", c(20, 40, 60, 80)))
#head of the data set with 40% of missing 
head(amp_df_list$prop40)
       AGE       OUT SUBJID
1 34.39524  74.58236 SUBJ-1
2 37.69823 100.53412 SUBJ-2
3 55.58708        NA SUBJ-3
4 40.70508  94.45932 SUBJ-4
5 41.29288  83.55338 SUBJ-5
6 57.15065        NA SUBJ-6

Similarly, we have the starting complete data set.

Code 
df_complete <- readRDS("../stats_ampute/amp_starting_complete_df.rds")
head(df_complete)
  SUBJID      AGE       OUT
1 SUBJ-1 34.39524  74.58236
2 SUBJ-2 37.69823 100.53412
3 SUBJ-3 55.58708 126.24033
4 SUBJ-4 40.70508  94.45932
5 SUBJ-5 41.29288  83.55338
6 SUBJ-6 57.15065 133.40075

Point estimate

In the clinical trial setting you may have longitudinal data, and you may certainly be willing to estimate the difference in the outcome (i.e Change from baseline) between different treatment groups in an specific time point. However, a very simple point estimate is good enough to acquire this knowledge. The slope’s coefficient of the linear regression OUT ~ AGE will be the point estimate in this post. A point estimate by using the completed data set will be obtained in the following chunk of code. This will be our true/reference estimate for the later steps. We simulated the starting data set under the alternative hypothesis where there is an statistically significant age effect in the OUT variable under a significance level of alpha = 0.05.

Let’s get the true point estimate we would have obtained in the absence of missing data.

Code 
fit_true <- lm(OUT ~ AGE, data = df_complete)
fit_true_ci <- janitor::round_half_up(confint(fit_true, "AGE", 0.95), 3)
summary_fit_true <- summary(fit_true)
coef_true <- summary_fit_true$coefficients[2, 1]
se_true <- summary_fit_true$coefficients[2, 2]
fit_true_df <- data.frame(
  missing_prop = "Complete", 
  point_est = coef_true, 
  "se" = se_true, 
  "ci_lower" = fit_true_ci[1], 
  "ci_upper" = fit_true_ci[2]
  )
fit_true_df
  missing_prop point_est        se ci_lower ci_upper
1     Complete  2.062202 0.3083317    1.442    2.682

The point estimate and the corresponding standard error are 2.0622024 and 0.3083317, respectively. It is up to you reducing/increasing the standard error by tweaking the OUT ~ AGE correlation when simulating the data 🙂.

Handling missing data

Before talking about the multiple imputation and its associated between sample variance that I am willing to showcase in this post, worth first mentioning the non desired methodologies to handle missing data when missing data is under MAR condition, which is the condition under which we simulated missingness. Keep in mind the following anticipated statement before we go into the non-desired methodologies: The standard error of the point estimate obtained from the imputed data set, should not be lower than the original complete data set. Also, no need to highlight the point estimate should be unbiased.

The non desired imputation approach example under MAR: Single unconditional mean imputation

Taking a look at the next table and figure (complete row contains the true estimates), we can conclude the single mean imputation (under MAR missingness) can have a negative impact when it comes to statistical inference. As the missing proportion increases, and under the simulated alternative hypothesis (AGE has an effect in the outcome):

  • Introduces increasing negative bias as a function of missing proportion in the point estimate, where the 95% CI of the imputed data sets with significant proportion of missingness is not even taking the true point estimate within it (bad coverage). After reading this post you should be able to know why this is happening🙂.
  • The standard error (and thereby the 95%CI) decreases as a function of missing proportion. As you may agree, this makes not sense at all, as missingness should, in any case, generate more uncertainty in the point estimate, right? 🤔 This is a very important point that we always have to keep in mind when it comes to statistical inference.

Under MCAR, the mean imputation may not unbias the estimate, but it is not a condition we can assume many times in the field I work, as missingness and thereby the non-observed values potentially depend on other variables (i.e in clinical trials assuming the missing outcome can depend on the baseline characteristics added as covariates in the model, which would be the MAR assumption) or even on the variable itself.

Code 
results_mean_imp <- sapply(amp_df_list, FUN = function(amp_df) {
  amp_df <- amp_df %>%
    select(-SUBJID)
  #showing you can also go over the single mean imputations by using mice
  #you can get the complete data sets by using mice::complete()
  imp_df <- complete(mice::mice(amp_df, method = "mean", m = 1, maxit = 1, printFlag = FALSE))
  fit_imp_mean <- lm(OUT ~ AGE, data = imp_df)
  summary_fit_imp_mean <- summary(fit_imp_mean)
  ci <- janitor::round_half_up(confint(fit_imp_mean, 'AGE', level=0.95), 3)
  c("point_est" = summary_fit_imp_mean$coefficients[2, 1], 
    "se" = summary_fit_imp_mean$coefficients[2, 2],
    "ci_lower" = ci[1],
    "ci_upper" = ci[2]
    )
}) %>%
  #making use the function defined at the top of the post 
  tidy_estimates_df() 

results_mean_imp <- fit_true_df  %>%
  rbind(results_mean_imp)


DT::datatable(results_mean_imp)
Code 
#making use the function defined at the top of the post 
plot_estimates(results_mean_imp)

Multiple imputation

As shown in the previous section, we may have a hard time if we use single imputation methods (can be either mean, median, linear regression) to handle missing data under MAR due to a potential bias as well as the underestimation of the standard error (precision). This is when we start talking about the Multiple Imputation and the Between-sample variance which is the main topic I would like to highlight in this post.

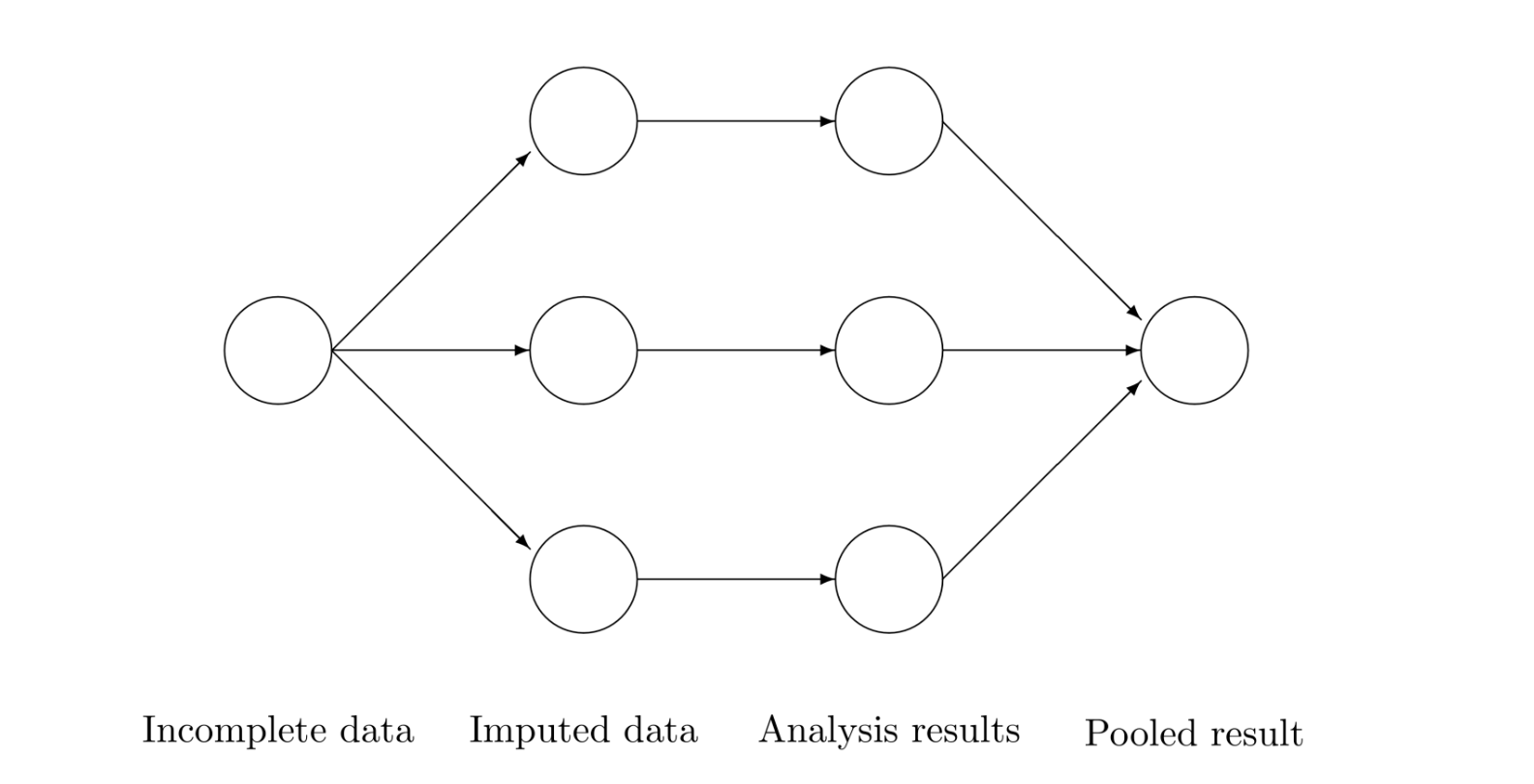
Donald B. Rubin (1) observed that imputing one value (single imputation) for the missing value could not be correct in general, and this is when he started thinking about creating multiple imputations to be able to reflect uncertainty of the missing data. The three main steps (imputation + analysis + pooling) that compose the multiple imputation procedure are explained in the following sections. The following figure taken from van Buuren (2) describes the process.

mice::mice() function will be used for this process.

Imputing data sets

We will create m = 100 number of imputed data sets by the chosen imputation model, leading to 100 number of complete data sets. In this post we will creating a high number of imputed data sets so that the later between-sample distributions can be more beautifully visualized in the later sections.

See some of the key parameters in the mice::mice function.

  • m: Number of imputed data sets to be created. 5 is the by default option.
  • method: A very important parameter where you state the imputation method to be used. For instance, we used the unconditional single mean imputation method before to share an example of a not-the-best imputation method (method = mean) under MAR. In this example I will be using the Bayesian Linear Regression. Do not worry about this point for now, just think we will be using the posterior distributions of the regression parameters to get the imputed values.
  • predictorMatrix: With the predictor matrix defined in the following chunk, I am stating the Age is going to be the predictor when imputing the outcome variable. No other imputation needed in our example.
Code 
predictor_matrix <- matrix(c(0, 0,
                             1, 0)
                           , nrow = 2, byrow = TRUE)

colnames(predictor_matrix) <- c("AGE", "OUT")

rownames(predictor_matrix) <- c("AGE", "OUT")

Let’s go over the first step of generating 100 imputed data sets per missing proportion under analysis.

Code 
amp_df_list_no_subj <- lapply(amp_df_list, FUN = function(mylist) {
  mylist %>% select(-SUBJID)
})
imp_list <- lapply(amp_df_list_no_subj, FUN = function(df) {
 mice::mice(df, m = 100, predictorMatrix = predictor_matrix, method = "norm", print = FALSE)
})

mice::mice creates an object of class mids.

Code 
class(imp_list$prop20)
[1] "mids"

Please take a look at the other elements returned by the mids object. For instance, you can see the imputation equations that have been used so that you can make sure mice has been gone over your desired approach.

Code 
imp_list$prop20$formulas
$AGE
AGE ~ 0
<environment: 0x142762098>

$OUT
OUT ~ AGE
<environment: 0x142762098>

You can also confirm you have been introducing the predictor matrix correctly:

Code 
imp_list$prop20$predictorMatrix
    AGE OUT
AGE   0   0
OUT   1   0

Applying the analysis model to each of the imputed data sets

In the next chunk of code we will be applying our target analysis model to each of the imputed data sets obtaining as many point estimates as imputed data sets (100 per missing proportion under analysis in our specific example). See the estimates of one of the regressions out of 400 we are generating.

Code 
imp_analysis_list <- lapply(imp_list, FUN = function(imp_dfs) {
  analysis <- with(imp_dfs, lm(OUT ~ AGE))
})

#showing one lm result out of 400 we generated 
summary(imp_analysis_list$prop20$analyses[[1]])

Call:
lm(formula = OUT ~ AGE)

Residuals:
    Min      1Q  Median      3Q     Max 
-40.084 -14.109   0.717  14.489  43.152 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -0.6083    11.4709  -0.053    0.958    
AGE           2.4071     0.2773   8.682  2.1e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 17.97 on 48 degrees of freedom
Multiple R-squared:  0.6109,    Adjusted R-squared:  0.6028 
F-statistic: 75.37 on 1 and 48 DF,  p-value: 2.096e-11

Pooling the m point estimates and standard errors.

Finally we pool/combine the by missing proportion specific m repeated complete-data point estimates (coefficients indicating the effect of age in the outcome) and variances. In this way we will have the average coefficient as the final effect, and the total variance that will account for the uncertainty due to missing data.

Code 
#Here we are getting the parameters such as the pooled estimates, within and between sample variances. 
pooled_estimates_list <- lapply(imp_analysis_list, FUN = function(imp_analysis) {
 mice::pool(imp_analysis)
})

#rerunning this to get the confidence intervals
pooled_estimates_list_ci <- lapply(imp_analysis_list, FUN = function(imp_analysis) {
 summary(mice::pool(imp_analysis), conf.int = TRUE)
})

#see the pooled results
pooled_estimates_list_ci
$prop20
         term  estimate  std.error statistic       df      p.value      2.5 %
1 (Intercept) -3.612254 15.0291997 -0.240349 25.50698 8.119809e-01 -34.534304
2         AGE  2.465793  0.3866069  6.378037 22.32632 1.899471e-06   1.664698
     97.5 %
1 27.309797
2  3.266888

$prop40
         term  estimate  std.error statistic       df    p.value       2.5 %
1 (Intercept) 15.697029 16.9789242 0.9245008 17.17583 0.36803280 -20.0974555
2         AGE  1.859607  0.4566897 4.0719262 13.84779 0.00116759   0.8790938
    97.5 %
1 51.49151
2  2.84012

$prop60
         term   estimate  std.error  statistic       df      p.value      2.5 %
1 (Intercept) -18.391875 18.4222489 -0.9983513 18.18803 3.312069e-01 -57.066924
2         AGE   2.875304  0.4891474  5.8781951 15.02825 3.011279e-05   1.832882
     97.5 %
1 20.283173
2  3.917726

$prop80
         term   estimate std.error    statistic       df   p.value       2.5 %
1 (Intercept) -0.1135468 52.575938 -0.002159673 6.677371 0.9983399 -125.664009
2         AGE  2.6986380  1.582285  1.705532156 4.364364 0.1572897   -1.553557
      97.5 %
1 125.436915
2   6.950833

For the confidence interval calculation of the pooled estimates, I would recommend going over the sections 9.3, 9.4 and 9.5 sections from the Applied Missing Data analysis with SPSS and R book (3).

Looking at the list above and the plot below, we can highlight the following:

  • Multiple imputation (unlike the unconditional single mean imputation) is providing unbiased point estimates throughout the entire spectrum of proportion of missingness evaluated.
  • The uncertainty increases (standard error or confidence interval) as a function of proportion of missingness. This is a fair point, right?
  • The uncertainty of the point estimates obtained after imputation is always higher than the uncertainty of the point estimate obtained with the complete data set. This will lead to a power loss (as expected), where in case of 80% of missing cases (a very edge case) the null hypothesis of age not impacting the OUT variable would not be even rejected (see the 95%CI whiskers taking the 0 value or the Age effect’s p-value < 0.05 in the above list) under a significance level of alpha = 0.05. Anyways, we’d rather go over a wide confidence interval than a narrow one with huge bias and very low coverage rate we got from the single mean imputation! Please take a look at section 2.5.2 from van Buuren’s book (2) to see the different evaluation criteria you can use to test the performance of the imputation processes tried in your simulations.
Code 
#tidying the above list
results_mi <- fit_true_df %>%
  bind_rows(do.call(rbind, pooled_estimates_list_ci) %>%
  filter(term == "AGE") %>%
  select(point_est = estimate, se = std.error, ci_lower = `2.5 %`, ci_upper = `97.5 %`) %>%
  bind_cols(missing_prop = c("prop20", "prop40", "prop60", "prop80")))
Code 
#using the function defined in the beginning of the report.
plot_estimates(results_mi)

Total variance in the multiple imputation

Explaining total variance calculation in the multiple imputation process is my ultimate goal in this post.
For this aim, demistifying the equation 2.17 from section 2.3 from Van Buuren’s book (2) by the use of some visualizations can be a good idea.

\[ V(Q|Y_{obs}) = \color{green}{E[V(Q|Y_{obs}, Y_{mis})|Y_{obs}]} + \color{red}{V(E(Q|Y_{obs}, Y_{mis})|Y_{obs})} = \color{green}{WithinSample} + \color{red}{BetweensSample} \]

Between sample variance

The between sample variance B shows the closeness of agreement between each imputed-complete individual point estimate (coefficient indicating the effect of age in the outcome) and the combined/pooled final point estimate that the MI process provides. You will see that the following equation is nothing but the well-known equation for calculating the sample variance. This is exactly the piece of the total variance that accounts for the uncertainty due to missing data. Single imputation basically ignore this important point! 🤦🏽‍♂️

\[ B = {1/(m - 1)}\sum_{j = 1}^{m} (est_j - \overline{est})^2 \] Where \(\overline{est}\) is the pooled average point estimate and m the number of imputed data sets. For instance, we obtained a between-sample variance of 2.2355279 in the MI process applied to a data set with 80% of the outcome values missing, as shown under the b term.

Code 
pooled_estimates_list$prop80[2, ]
Class: mipo    m = NA 
  term   m estimate      ubar        b        t dfcom       df      riv
2  AGE 100 2.698638 0.2457429 2.235528 2.503626    48 4.364364 9.187991
     lambda       fmi
2 0.9018452 0.9285019

You can see that calculating the variance of the 100 individual point estimates yields the same exact result we have above under the b term (between sample variance)! 🥇

Code 
sapply(imp_analysis_list$prop80$analyses, FUN = function(estimates_tmp) {
  estimates_tmp$coefficients[2]
}) %>%
  var()
[1] 2.235528

See the following figure with all the individual point estimates obtained from each of the imputed data sets, color coded by the starting missing proportion (100 imputed data sets for each missing proportion under analysis) along with the corresponding density plots. The dispersion/variation we see between the point estimates (within color) is exactly what the between-sample variance explains. As we concluded above, this uncertainty due to missing increases as the bigger is the starting missing proportion, as expected.

Code 
# Get the point estimate, standard error and confidence intervals. 
imp_estimates_list <- lapply(names(imp_analysis_list), FUN = function(miss_prop_tmp) {
  analysis_list <- imp_analysis_list[[miss_prop_tmp]]
  analysis_list <- analysis_list$analyses
  do.call(rbind, sapply(analysis_list, FUN = function(analysis_tmp) {
  summary_fit_tmp <- summary(analysis_tmp)
  ci <- janitor::round_half_up(confint(analysis_tmp, 'AGE', level=0.95), 3)
  list(c("point_est" = summary_fit_tmp$coefficients[2, 1], 
    "se" = summary_fit_tmp$coefficients[2, 2],
    "ci_lower" = ci[1],
    "ci_upper" = ci[2]
    ))
  })) %>%
    bind_cols(data.frame(miss_prop = rep(miss_prop_tmp, 100), 
                         imp = paste0("imp", seq(1, 100)))) %>%
    mutate(imp = factor(imp, levels = paste0("imp", seq(1, 100))))
})


imp_estimates_df <- do.call(rbind, imp_estimates_list) 

plot_estimates(
    df = imp_estimates_df, 
    title = "Point estimates and 95%CI by missing proportion",
    imputations = TRUE,
    group = "miss_prop",
    type = "density",
    xlab = "1 to 100 imputed data sets")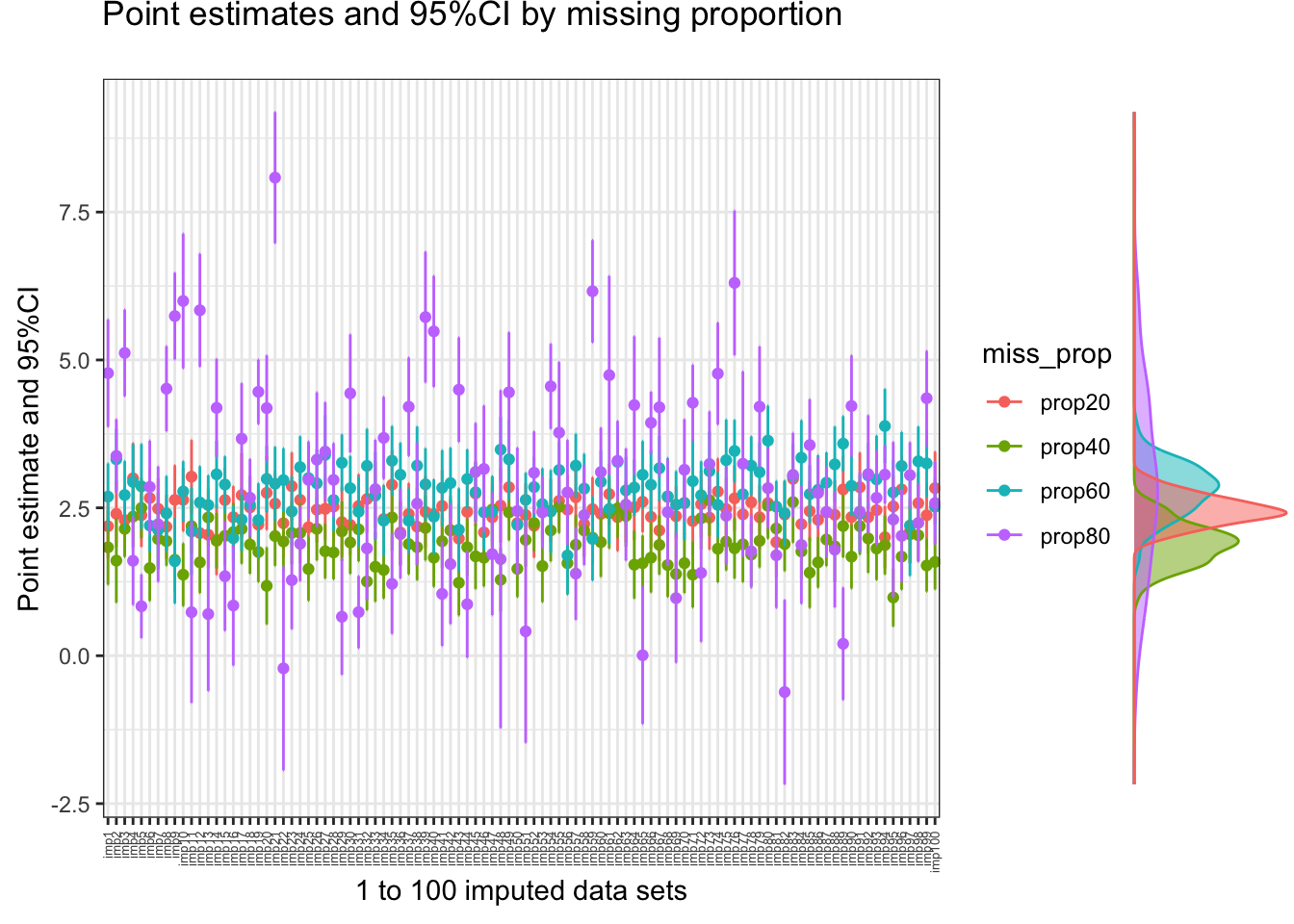

Within sample variance

The within sample variance is nothing but the average of the repeated complete-data posterior variances of the point estimate. For instance, for the 80% of missing proportion case, we are getting the within sample variance of 0.2457429. In the following code chunk we are trying to get the same value by obtaining the individual estimate uncertainty values and calculating the average. Again, we are able to get the same exact value. 🤛🏽

Code 
sapply(imp_analysis_list$prop80$analyses, FUN = function(estimates_tmp) {
  summary_tmp <- summary(estimates_tmp)
  summary_tmp$coefficients[2,2]^2
}) %>%
  mean()
[1] 0.2457429

Third source of variation to consider when estimating the total variation

When the number m of multiply imputed data sets is quite low, we need to consider the additional third between sample variance / m term to account for the low number of imputed data sets used for getting the pooled point estimate. By default, mice uses an m of 5, but we have been using an m of 100. Section 2.8 fron van Buuren (2) talks about the optimal number of multiply imputed data sets to be created.

Recap

These are the main topics we have covered so far in this post.

  • Presented a simple example to showcase single mean imputation can drive us nuts under MAR missingness. Keep in mind we have been working with the missing data sets we simulated in this post under different missing proportions and that we only generated univariate missing data in the OUT variable conditional on AGE variable (MAR).
  • Went over the 3 Rubin’s imputation + analysis + pooling general steps that compose the multiple imputation process. Did not go deep on the imputation method used in as this was not the intention of this post.
  • Compared the single imputation VS multiple imputation results as a function of different missing proportions.
  • Highlighted the between-sample variance term and its importance to account for the uncertainty due to missingness This was my main goal on this post. Hopefully I achieved it!

I spent some time of my long flight to San Francisco to work on this post. Cannot wait to meet my colleagues from Denali Therapeutics in person again! Exciting as well as intense week ahead. Let’s get it!

Picture taken from Mount Tamalpais.

References

1.
D. B. Rubin, Multiple imputation for nonresponse in surveys (Wiley, 1987).
2.
, Https://stefvanbuuren.name/fimd/ (March 10, 2024).
3.
, Chapter9 Rubin’s Rules Book_MI.knit (March 10, 2024).